Нюансы реализации

Однозначное соответствие примитива узлу

Вообще, алгоритм разбиения пространства имеет в реализации ряд спорных и сложных моментов, которые разработчики решают на своё усмотрение.

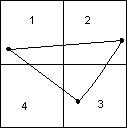
Например, вот ситуация (рис. 5), когда один примитив, при разбиении октарным деревом, относится сразу к 4м листам.

В этом случае нельзя относить этот примитив к какому-то одному листу, т. к. если примитив отнести к 3 листу, и этот лист не попадёт в область видимости, а листы 1, 2, 4 будут видны, то треугольник виден не будет. Что является ошибкой.

Если отнести примитив сразу к 4м листам, и они сразу все будут видны, то этот примитив будет выводиться четыре раза подряд. Несмотря на это, такие реализации применяются довольно часто [7]. Если таких примитивов много, и они покрыты текстурами, то все преимущества октарных деревьев очень мало проявляются.

Ситуацию, когда один примитив, при разбиении октарным деревом, относится сразу к нескольким листам, можно решить несколькими способами. Сначала создаём дерево из примитивов, которые полностью входят в листья дерева. Из тех примитивов, которые не входят в листья, составляется массив который в самом простом случае просто выводится на экран.

Нами предлагается более рациональное решение - сделать возможность присвоения примитивов не только листьям, а и узлам деревьев. Тогда, если примитив не может быть однозначно присвоен листу, он должен быть присвоен узлу, которому принадлежит этот лист (Но при этом примитив должен однозначно вписываться в границы этого узла).

Еще одна проблема традиционного алгоритма - примитивы нельзя относить к узлу только по координатам их вершин. На рис. 5 вершины треугольника расположены в узлах 1, 2, 3, а сам треугольник находится в узлах 1, 2, 3, 4. Возможен частный случай, когда видим будет только узел 4, а 1, 2, 3 будут не видны. Тогда треугольник отображаться не будет. Что тоже является ошибкой. Эта проблема не существует в модифицированном нами алгоритме, так как там примитивы однозначно присваиваются узлам.