Скорость работы алгоритмов

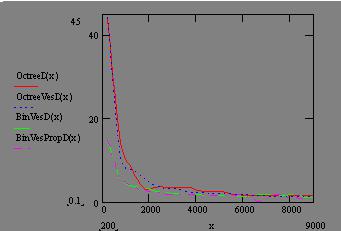
Рассмотрим, какой алгоритм имеет лучшие показатели FPS. Для этого проведём эксперименты, меняя глубину разбиения, и точку зрения наблюдателя. На рис. 11, рис. 12, меняется максимально допустимое количество примитивов в листе от 200 до 101000, с шагом приращения в 500 примитивов. При этом у октарного дерева (OctreeD) максимальная равна 0, 8, у весового бинарного пропорционального (BinVesPropD) (BVPD) 0, 57, у бинарного весового (BinVesD) 0, 68, у октарного весового (OctreeVesD) 0, 59.

Тесты проводились на компьютере с конфигурацией Athlon 2000, 512мб, Video - Radeon 9600 Pro 128 Mb, OS Windows XP. Графики строились и интерполировались с помощью программы Mathcad.

Октарное и бинарное весовое пропорциональное деревья занимают лидирующее положение по FPS (рис. 11, рис. 12). Поэтому рассмотрим дополнительно рис. 13, на котором максимально допустимое количество примитивов меняется от 200 до 3000, и шаг приращения равен 100. У первого дерева максимальная равна 2, 70, у второго 1, 19. Октарное дерево при уменьшении максимально допустимого количества примитивов в листе демонстрирует постоянный прирост FPS, а у бинарного весового пропорционального FPS меняется скачками. Хотя максимальные значения FPS у этих алгоритмов почти равны, но найти максимальное значение FPS у алгоритма октарного дерева значительно проще, так как значение FPS у этого алгоритма максимально при максимально допустимом количестве примитивов в листе около 300. Поэтому при использовании бинарных весовых деревьев нужно искать этот максимум FPS для более эффективного использования алгоритма. К тому же, экстремумов FPS бывает несколько, что усложняет поиск максимума.

На рис. 14 показана зависимость времени разбиения сцены различными алгоритмами, от глубины разбиения. Как видно, бинарному весовому пропорциональному дереву требуется меньше всего времени для разбиения сцены. Больше всего времени требует октарное дерево. После максимально допустимого количества примитивов в листе, от начиная от 9000, алгоритмы показывают примерно одинаковое время, поэтому на графике этого не изображено. Максимальная времени создания дерева для всех алгоритмов, изображённых на рис. 14, не превышает 1, 7.

Проверим предположение, зависит ли скорость алгоритма от того, как удачно входят в пирамиду видимости узлы или листья. Отношение количества видимых узлов ко всем узлам, и видимых листов ко всем листьям примерно одинаково при 30% видимости сцены. Но у октарного дерева и бинарного весового пропорционального дерева этот показатель чуть ниже, это обуславливает его лучшие показатели FPS. Между отношением количества видимых узлов ко всем узлам, видимостью листов ко всем листьям и FPS есть хорошо заметная зависимость. Чем ниже эти показатели, тем выше FPS.